COMPETENCIA MATEMÁTICA, UN
APRENDIZAJE FUNDAMENTAL
Prof. Carlos A. Yampufé Requejo
DNI 16692033
En la Unión europea la Competencia Matemática es
una de las competencias clave para el aprendizaje permanente. “Las
Competencias Clave representan un paquete multifuncional y transferible de conocimientos,
destrezas y actitudes que todos los individuos necesitan para su realización y
desarrollo personal, inclusión y empleo. Éstas deberían haber sido
desarrolladas para el final de la enseñanza o formación obligatoria, y deberían
actuar como la base para un posterior aprendizaje como parte de un aprendizaje
a lo largo de la vida”[1].
La definición enfatiza que las competencias clave deberían ser transferibles, y
por tanto aplicables en muchas situaciones y contextos, y multifuncionales, en
tanto que pueden ser utilizadas para lograr diversos objetivos, para resolver
diferentes tipos de problemas y para llevar a cabo diferentes tipos de tareas.
Las competencias clave son un prerrequisito para un rendimiento personal
adecuado en la vida, en el trabajo y posterior aprendizaje.
Bajo la propuesta de las Rutas del Aprendizaje, los
Aprendizajes Fundamentales “Son competencias generales, que
todos los estudiantes peruanos sin excepción necesitan lograr y tienen derecho
a aprender, desde el inicio hasta el fin de su educación básica. Por lo tanto,
el Estado garantiza las condiciones para que todas ellas puedan enseñarse y
aprenderse de manera efectiva en todo el territorio nacional.”
DEFINICIÓN
DE COMPETENCIA MATEMÁTICA EN PISA[2]
El conocimiento matemático es esencial para la
preparación de los jóvenes para la vida en la sociedad moderna ya que una
creciente proporción de problemas y situaciones que se presentan en el trabajo
y contextos profesionales, requieren razonamiento de cierto nivel, utilización
de estrategias y herramientas matemáticas. Por tanto es importante tener una
comprensión de qué tan preparados están los jóvenes que egresan de la educación
básica para aplicar Matemática, para entender cuestiones que la involucran y
resolver problemas significativos.
Como base para el reconocimiento de la Competencia
Matemática, es razonable preguntar:
·
¿qué es importante para las personas conocer y
saber hacer en situaciones que involucran Matemática?
·
¿qué significa ser competente en Matemática para
un joven, que podría estar egresando de la enseñanza básica o preparándose para
seguir una formación específica para una carrera u oficio o ingresar en la
Universidad?
Es importante que el concepto de competencia
matemática, que es utilizado en este documento para señalar la capacidad de los
individuos para formular, aplicar e interpretar Matemática en contextos
variados, no sea percibido como sinónimo de conocimientos y destrezas mínimas o
de bajo nivel. Por el contrario, está pensado en base a las capacidades de los
individuos para razonar matemáticamente y aplicar conceptos matemáticos,
procedimientos, datos y herramientas para describir, explicar y predecir
fenómenos. Una premisa de PISA es que, con el fin de mejorar las posibilidades
de éxito en la vida adulta, es necesario que la educación Matemática que
reciban los estudiantes les brinde las oportunidades de experimentar cómo la
Matemática es usada en una variedad de contextos, no solamente áulicos. Esta
posición no niega la importancia para los estudiantes del desarrollo de una
sólida comprensión de conceptos de la Matemática pura, ni de lo beneficioso que
es para ellos involucrarse en exploraciones en el mundo abstracto de la
Matemática o de desarrollar alto nivel de destreza algorítmica. Sin embargo, la
construcción de la competencia matemática, como la define PISA, llama al
equilibrio desarrollando también en los estudiantes la capacidad de usar
Matemática en contextos auténticos para lo que es importante que tengan ricas
experiencias en clase que acompañe ese desarrollo. Se agrega a lo anterior que
para casi todos los alumnos, la motivación para aprender Matemática es mayor
cuando ven la importancia y la utilidad de lo que están aprendiendo. La
Competencia matemática no es un atributo que un individuo tiene o no tiene sino
que es un atributo que está en proceso continuo de desarrollo; algunos
individuos se muestran matemáticamente más competentes que otros y todos poseen
el potencial de desarrollar esta habilidad.
“La capacidad del individuo para formular, emplear e interpretar
las matemáticas en distintos contextos. Incluye el razonamiento matemático y la
utilización de conceptos, procedimientos, datos y herramientas matemáticas para
describir, explicar y
predecir fenómenos. Ayuda a los individuos a reconocer el papel
que las matemáticas desempeñan en el mundo y a emitir
los juicios y las decisiones
bien fundadas que los ciudadanos constructivos, comprometidos y reflexivos
necesitan.
El foco de la definición de competencia
matemática está en la participación activa en la Matemática y
hace énfasis en el razonamiento matemático y el uso de conceptos,
procedimientos, datos, y herramientas para describir, explicar y predecir
fenómenos. En particular, los verbos “formular”, “emplear”, e “interpretar”
apuntan a los tres procesos que los estudiantes activarán como diligentes
solucionadores de problemas.
Modelización
en Matemática
La definición de competencia
matemática integra la noción de modelización matemática, que ha sido
históricamente uno de los pilares del marco conceptual de la evaluación en
Matemática en PISA. El esquema presenta cómo los individuos utilizan la
Matemática y sus herramientas para resolver problemas contextualizados, así
como también el avance de su trabajo a través de una serie de etapas. El
proceso de modelización matemática empieza con el planteo de un “problema en
contexto”. Quien se enfrenta a resolver un problema identifica la matemática
relevante en la situación planteada y formula
la situación matemáticamente de acuerdo a los conceptos y relaciones
identificados. Transforma el “problema en contexto” en un “problema formulado
matemáticamente” susceptible de tratamiento matemático. La siguiente etapa del
proceso describe el trabajo realizado por la persona que se plantea el desafío
de resolver el problema: emplea
conceptos matemáticos, procedimientos, datos y herramientas para encontrar el
“resultado matemático”. Esta etapa generalmente implica razonamiento,
manipulación, transformación y cálculo. Luego, los “resultados matemáticos”
deben ser interpretados
en términos del problema original: “resultados en contexto”. Esto supone la
interpretación, aplicación y evaluación de los resultados matemáticos y su
pertinencia en el contexto auténtico en que se basa el problema. Estos procesos
de formulación,
uso e interpretación matemática son componentes clave en el ciclo de
la modelización matemática y también son componentes clave en la definición de
competencia matemática.
Competencia Matemática en acción
La descripción del ciclo de modelización matemática
anterior presenta un panorama idealizado y simplificado de la competencia
matemática. Es un esquema de como se
observa en la práctica, aunque con frecuencia no es necesario incursionar en
todas las etapas del ciclo de modelización al resolver un problema. A menudo se
da el caso de que partes significativas del ciclo de modelización matemática
han sido realizadas por otros, y el usuario final lleva a cabo algunas etapas
del ciclo, pero no todas ellas. Por ejemplo, en algunos casos, representaciones
matemáticas como gráficos o ecuaciones, son dadas para que puedan ser
manipuladas directamente con el fin de responder algunas preguntas o sacar
algunas conclusiones. Por esta razón. En realidad, quien se plantea resolver el
problema también puede a veces oscilar entre los procesos y las etapas,
volviendo a revisar decisiones y supuestos anteriores. Cada una de las etapas
puede presentar desafíos considerables y pueden requerir varias iteraciones del
ciclo completo.
La referencia a “una
variedad de contextos” en la definición de la competencia
matemática es intencional entendido como una forma de vincular los
contextos específicos, (personales, ocupacionales, sociales y científicos) que
serán descriptos y ejemplificados más adelante en este documento y se utilizan
para reflejar una amplia gama de situaciones en las que los individuos pueden
encontrar oportunidades de matematizar.
La definición de competencia matemática
explícitamente incluye el empleo
de herramientas matemáticas. Estas herramientas abarcan una
variedad de equipos físicos y digitales, como software y calculadoras. Las
herramientas informáticas son de uso común en los lugares de trabajo del siglo
XXI y serán cada vez más frecuentes a medida que avance el siglo. La naturaleza
de los problemas relacionados con el trabajo y el razonamiento lógico se han
expandido con estas nuevas oportunidades de creación de nuevos escenarios para
la puesta en marcha de la competencia matemática.
DIMENSIONES
DE LA COMPETENCIA MATEMÁTICA
Estas dimensiones evalúan hasta qué punto los
estudiantes se manejan hábilmente en Matemática cuando se enfrentan con
situaciones y problemas que habitualmente son presentados en contextos
auténticos.
A los efectos de la evaluación, la definición de
competencia matemática en PISA 2012 puede ser analizada en términos de tres
aspectos interrelacionados:
·
El contenido
matemático que las actividades de prueba abordan.
·
Los procesos
matemáticos que describen lo que es necesario hacer para conectar el contexto del
problema con la Matemática que está implícita en él y así resolverlo, y las
capacidades que subyacen a esos procesos.
·
Los contextos
en los cuales los ítemes de evaluación se sitúan.
Las actividades propuestas en el desarrollo de la
competencia matemática deben reflejar una gama de contenidos, procesos y
contextos que efectivamente ponen en práctica las dimensiones dela definición
de la competencia matemática. Son varias las preguntas que sustentan esta
definición de competencia matemática:
·
¿Qué conocimiento del contenido matemático se
puede esperar de las personas en general y de los estudiantes en particular?
·
¿Qué procesos ponen en marcha los individuos
comprometidos cuando resuelven problemas de contenido matemático, y qué
capacidades esperamos que los individuos sean capaces de demostrar cuando
aumenta el nivel de competencia matemática?
·
¿En qué contextos la competencia matemática
puede ser observada y evaluada?
Contenido Matemático
Para los ciudadanos del mundo actual es importante
la comprensión del contenido matemático y la habilidad de aplicarlo a la
resolución de problemas significativos y contextualizados. Para resolver
problemas e interpretar situaciones en diversos contextos de la vida es
necesario recurrir a ciertos conocimientos matemáticos.
Las estructuras matemáticas se han desarrollado
históricamente para entender e interpretar fenómenos naturales y sociales. En
la enseñanza formal el currículum de Matemática suele organizarse en torno a
ramas de contenido (ej. Número, Álgebra, Geometría) y listas detalladas de
temas que ayudan a definir un currículum estructurado. Sin embargo, fuera de la
clase de Matemática, una situación que surge no suele estar acompañado por un
conjunto de reglas y fórmulas que muestren como debe enfrentarse. Por lo
general requiere pensamiento más o menos creativo en la formulación matemática
de la situación y con frecuencia el uso de ramas de conocimiento que involucran
múltiples contenidos. En ocasiones la situación puede ser abordada de
diferentes maneras recurriendo a diferentes conceptos matemáticos,
procedimientos, datos o herramientas.
Dado que el objetivo es el desarrollo de la
competencia matemática en los estudiantes, se propone una estructura para
organizar los contenidos basada en fenómenos matemáticos que subyacen en
grandes clases de problemas y que han motivado el desarrollo de determinados
conceptos y procedimientos matemáticos. Por ejemplo, fenómenos matemáticos como
los de cambio y relaciones e incertidumbre subyacen en muchas situaciones que
ocurren comúnmente, por lo que se han desarrollado estrategias y herramientas
matemáticas para analizarlos. Esta organización de contenido no es nueva, como
se ejemplifica en dos conocidas publicaciones: Sobre los Hombros de Gigantes
(Steen, 1990) y Matemática: La Ciencia de los patrones (Devlin, 1994).
Por lo tanto, se ha seleccionado un conjunto de
categorías de contenido que reflejan la variedad de fenómenos matemáticos
subyacentes, en consonancia con las categorías utilizadas para estudios previos
de PISA.
La siguiente lista de categorías de contenido es
utilizada para cumplir con los requerimientos del desarrollo histórico, la
cobertura del dominio de Matemática y los fenómenos subyacentes que generan el
desarrollo de los ejes principales del currículum escolar. Estas cuatro
categorías caracterizan el rango de contenido matemático que es el centro de la
disciplina e ilustran las amplias áreas de contenido que guían el desarrollo de
las actividades que desarrollan la competencia matemática.
·
Cantidad
·
Espacio y forma
·
Cambio y relaciones
·
Incertidumbre y datos
Mientras que la clasificación por categorías de
contenido es indispensable tanto para el desarrollo y la selección de los
contenidos, es importante notar que algunos tópicos específicos de contenido
pueden materializarse en más de una de las categorías. Por ejemplo, un ítem
aplicado en una de las primeras ediciones de PISA llamado “Las Pizzas” propone
determinar cuál de dos pizzas redondas, con diferentes diámetros y diferentes
precios pero el mismo grosor, tiene el precio más conveniente. Este ítem aborda
distintas áreas de contenido Matemático tales como geometría, pues refiere a
dos círculos; su solución implica cálculos aritméticos en términos de precios,
razonamiento proporcional y relación entre variables asociadas a la superficie
y el costo de cada pizza. Claramente, por referirse a figuras geométricas, éste
ítem podría haber sido clasificado como un ítem de Espacio y forma. Sin embargo
este ítem fue clasificado en la categoría Cambios y relaciones ya que la clave
del problema radica en que los estudiantes sean capaces de relacionar las áreas
de las dos pizzas que tienen distinto diámetro y su relación con el precio, lo
que implica razonamiento proporcional.
A continuación se presentan, en primer lugar, las
descripciones de cada categoría de contenido y su importancia para resolver
problemas significativos, seguido de definiciones más específicas del tipo de
temas que se consideraron apropiados para incluir en una evaluación de
competencia matemática a estudiantes. Estos temas específicos reflejan los acuerdos
encontrados a partir de las expectativas de los países participantes en la
evaluación, así como de ciertas jurisdicciones educativas.
Cantidad
La noción de cantidad incorpora la
cuantificación de los atributos de los objetos, las relaciones, las situaciones
y las entidades del mundo, interpretando distintas representaciones de esas
cuantificaciones y juzgando interpretaciones y argumentos basados en la
cantidad. Participar en la cuantificación del mundo supone comprender las
mediciones, los cálculos, las magnitudes, las unidades, los indicadores, el
tamaño relativo y las tendencias y patrones numéricos. Algunos aspectos del
razonamiento cuantitativo, como el sentido de número, las múltiples
representaciones de estos, la elegancia en el cálculo, el cálculo mental, la
estimación y evaluación de la justificación de los resultados, constituyen la
esencia de la competencia matemática relativa a la cantidad.
La cuantificación es un método clave para describir
y medir un vasto conjunto de atributos del mundo. Permite modelizar
situaciones, examinar y cuantificar cambios y relaciones, describir y manipular
figuras y evaluar probabilidades. Por lo tanto la competencia
matemática en el área de Cantidad aplica los conocimientos
de número y operaciones numéricas en una amplia variedad de contextos.
Espacio
y forma
Espacio y forma
incluye una amplia gama de fenómenos que se encuentran en nuestro mundo visual
y físico: patrones, propiedades de los objetos, posiciones y direcciones, representaciones
de los objetos, decodificación y codificación de información visual, navegación
e interacción dinámica con formas reales, así como con representaciones. Se
presupone que la comprensión de un conjunto de conceptos y destrezas básicas es
importante para la competencia matemática relativa al espacio y la forma. La
competencia matemática en esta área incluye una serie de actividades tales como
la comprensión de la perspectiva (por ejemplo en los cuadros), la elaboración y
lectura de mapas, la transformación de las formas con y sin tecnología, la
interpretación de vistas de escenas tridimensionales desde distintas perspectivas
y la construcción de representaciones de formas. La Geometría actúa como base
esencial para Espacio y forma, pero la categoría se extiende más allá de la
geometría tradicional en cuanto al contenido, significado y método, a partir de
elementos de otras áreas de la Matemática como la visualización espacial, la
medición y el álgebra.
Cambio
y relaciones
El mundo a nuestro alrededor muestra múltiples relaciones
temporales y permanentes entre objetos y circunstancias, donde ocurren cambios
entre sistemas de objetos interrelacionados o en circunstancias en que los
elementos influyen unos con otros. En muchos casos estos cambios ocurren con el
tiempo, y en otros casos un cambio en un objeto o cantidad está relacionado con
cambios en otro. Siendo más literal, cambio y relaciones,
implica tipos fundamentales de cambios y el reconocimiento de cuándo ocurren
para utilizar modelos matemáticos adecuados para describirlos y predecirlos.
Matemáticamente esto significa modelizar el cambio y las relaciones con
funciones apropiadas, así como la creación, interpretación y traducción de
representaciones simbólicas y gráficas de las relaciones.
Cambio y relaciones
son evidentes en diversos entornos como crecimiento de organismos, música,
ciclo de las estaciones, patrones del clima y condiciones económicas, entre
otras. Aspectos de los contenidos matemáticos tradicionales sobre funciones y
álgebra, incluyendo expresiones algebraicas, ecuaciones e inecuaciones, tablas
y representaciones gráficas, son esenciales en la descripción, modelización e
interpretación de los fenómenos de cambio. La actividad Caminar
contiene dos preguntas que ejemplifican las categorías de Cambio y Relaciones
ya que el foco se centra en relaciones algebraicas entre dos variables. Los
estudiantes tienen que usar una fórmula que relaciona el largo de un paso con
el número de pasos por minuto —fórmula expresada algebraicamente— para
determinar el largo de un paso en una pregunta y la velocidad de la caminata en
la otra. Representaciones de los datos y relaciones descritas usando
estadística también suelen ser aplicadas para describir e interpretar cambios y
relaciones, y una base sólida en los fundamentos de número y unidades es
también esencial para definir e interpretar Cambios y relaciones.
Algunas relaciones interesantes surgen entre las magnitudes de figuras
geométricas, tales como la forma en que variaciones en el perímetro de una
familia de figuras puede relacionarse con variaciones en su área, o las
relaciones entre las longitudes de los lados de un triángulo.
Incertidumbre
y datos
La incertidumbre y datos
es un fenómeno central del análisis matemático de muchas situaciones de los
problemas, y la teoría de la incertidumbre y datos y la estadística, así como
las técnicas de representación y descripción de datos, se han establecido para
darle respuesta. Esta categoría incluye el reconocimiento del lugar de la
variación en los procesos, la posesión de un sentido de cuantificación de esa
variación, la admisión de incertidumbre y error en las mediciones, y los
conocimientos sobre el azar. Asimismo, comprende la elaboración, interpretación
y valoración de las conclusiones extraídas en situaciones donde la incertidumbre
y datos son fundamentales. La presentación e interpretación de datos son
conceptos clave en esta categoría.
Procesos Matemáticos
La definición de competencia matemática hace
referencia a la capacidad del individuo para formular, emplear e interpretar
las matemáticas. Estos tres términos ofrecen una estructura útil y
significativa para organizar los procesos matemáticos que describen lo que
hacen los individuos para relacionar el contexto de un problema con las
matemáticas y, de ese modo, resolverlo.
Formulación
matemática de las situaciones
En la definición de competencia matemática, el
término “formular”
hace referencia a la capacidad del individuo para reconocer e identificar
oportunidades para utilizar las matemáticas y, posteriormente, proporcionar la
estructura matemática a un problema presentado de forma contextualizada. En
concreto, este proceso incluye las siguientes actividades:
·
Identificación de los
aspectos matemáticos de un problema situado en un contexto del mundo real e
identificación de las variables significativas;
·
Reconocimiento de la
estructura matemática (incluidas las regularidades, las relaciones y los
patrones) en los problemas o situaciones;
·
Simplificación de una
situación o problema para que sea susceptible de análisis matemático;
·
Identificación de las
limitaciones y supuestos que están detrás de cualquier construcción de modelos
y de las simplificaciones que se deducen del contexto;
·
Representación
matemática de una situación, utilizando las variables, símbolos, diagramas y
modelos estándar adecuados;
·
Representación de un
problema de forma diferente, incluida su organización según conceptos
matemáticos y formulando los supuestos adecuados;
·
Comprensión y explicación
de las relaciones entre el lenguaje específico del contexto de un problema y el
lenguaje simbólico y formal necesario para representarlo matemáticamente;
·
Traducción de un problema
a lenguaje matemático o a una representación;
·
Reconocimiento de
aspectos de un problema que se corresponde con problemas conocidos o conceptos,
datos o procedimientos matemáticos; y
·
Utilización de la
tecnología (como una hoja de cálculo o funciones en una calculadora gráfica)
para representar una relación matemática inherente a un problema
contextualizado.
Empleo
de conceptos, datos, procedimientos y razonamientos matemáticos
En la definición de competencia matemática, el
término “emplear”
hace referencia a la capacidad del individuo para aplicar conceptos, datos,
procedimientos y razonamientos matemáticos en la resolución de problemas
formulados matemáticamente con el fin de llegar a conclusiones matemáticas. En
concreto, este proceso incluye actividades tales como:
·
El diseño e
implementación de estrategias para encontrar soluciones matemáticas;
·
La utilización de
herramientas matemáticas, incluida la tecnología, que ayuden a encontrar
soluciones exactas o aproximadas;
·
La aplicación de datos,
reglas, algoritmos y estructuras matemáticas en la búsqueda de soluciones;
·
La manipulación de
números, datos e información gráfica y estadística, expresiones algebraicas y
ecuaciones, y representaciones geométricas;
·
La realización de
diagramas, gráficos y construcciones matemáticas y la extracción de información
matemática de los mismos;
·
La utilización de
distintas representaciones para buscar soluciones posibles;
·
La realización de
generalizaciones basadas en los resultados de aplicar procedimientos
matemáticos para encontrar soluciones; y
·
La reflexión sobre
argumentos matemáticos y la explicación y justificación de los resultados
matemáticos.
Interpretación,
aplicación y valoración de los resultados matemáticos
El término “interpretar”,
utilizado en la definición de competencia matemática, se centra en la capacidad
del individuo para reflexionar sobre soluciones, resultados o conclusiones
matemáticas e interpretarlas en el contexto de los problemas de la vida real.
En concreto, este proceso de interpretación, aplicación y valoración de los
resultados matemáticos incluye actividades tales como:
·
La reinterpretación de un
resultado matemático en el contexto del mundo real;
·
La valoración de la
razonabilidad de una solución matemática en el contexto de un problema del mundo
real;
·
La comprensión del modo
en que el mundo real afecta a los resultados y cálculos de un procedimiento o
modelo matemático para realizar juicios contextuales sobre la forma en que los
resultados deben ajustarse o aplicarse;
·
La explicación de por qué
un resultado o una conclusión matemática tiene o no tiene sentido dado el
contexto de un problema;
·
La comprensión del
alcance y de los límites de los conceptos y las soluciones matemáticas; y
·
El análisis e identificación
de los límites del modelo utilizado para resolver un problema.
Capacidades
Matemáticas Fundamentales Subyacentes en los Procesos Matemáticos
Una década de experiencia en el desarrollo de las
actividades de prueba de PISA y en el análisis de las formas en que los
estudiantes responden a los ítemes han revelado que hay una serie de
capacidades matemáticas fundamentales que subyacen en cada uno de estos
procesos reportados y que también sustentan en la práctica la competencia
matemática. La obra de Mogens Niss y sus colegas daneses (Niss, 1999, 2003)
identifican siete capacidades como fundamentales para el uso instrumental de la
Matemática que fueron publicadas en el marco del área para el ciclo 2003.
Existe un amplio consenso sobre la necesidad de
identificar un conjunto de capacidades matemáticas generales para complementar
el papel que cumple el conocimiento de contenido matemático específico en el
aprendizaje de Matemática. Las capacidades esenciales de la competencia
matemática que se utilizan en este marco se ilustran en la figura.
Comunicar:
el concepto de Competencia matemática implica comunicación. El sujeto percibe
la existencia de un desafío y es estimulado a reconocer y entender una
situación problema. Leer, decodificar e interpretar algunas afirmaciones,
preguntas, tareas u objetos permiten al individuo formar un modelo mental de la
situación, lo que es un paso importante en la comprensión, clarificación y
formulación de un problema. Durante el proceso de resolución, la información
puede necesitar aún mayor interpretación y los resultados intermedios pueden
tener que ser resumidos y presentados. Una vez que se ha encontrado una solución
a la propuesta, puede ser necesario presentarla y quizás habrá requerimientos
de brindar una explicación o justificación.
Varios factores determinan el nivel y la dimensión
de la demanda de comunicación de una tarea, y la habilidad de la persona para satisfacer
esas demandas indica en qué medida ha desarrollado la capacidad de
comunicación. Para los aspectos receptivos de la comunicación, estos factores
incluyen la extensión y complejidad del texto u otro objeto a ser leído e
interpretado, la familiaridad de las ideas o información a la que se refiere el
texto u objeto, el grado en que la información requiere ser desligada de otra,
la organización de la información y los procesos de pensamiento requeridos para
interpretarla y utilizarla, así como la medida en que los diferentes elementos
que necesitan ser interpretados (textos, gráficos, tablas, cuadros) se
relacionan con los demás elementos presentes en la propuesta.
Para los aspectos expresivos de la comunicación, el
menor nivel de complejidad se observa en tareas que exigen simplemente dar una
respuesta numérica. Cuando se añade la exigencia de una respuesta, más extensa
por ejemplo cuando se requiere dar una explicación o justificación oral o
escrita, la exigencia en comunicación aumenta.
Matematizar:
La competencia matemática puede implicar transformar un problema definido en el
mundo cotidiano en una forma estrictamente matemática (que puede incluir
estructurar, conceptualizar, hacer suposiciones, formular un modelo) o
interpretar una solución matemática o un modelo matemático en relación con el
problema original en su contexto. El término matematización es utilizado para
describir las actividades matemáticas fundamentales implicadas en esos
procesos.
En algunas tareas, no se requiere matematización,
ya sea porque el problema ya se encuentra expresado en términos matemáticos, o
no se necesita la relación entre el modelo y la situación planteada para
resolver ni para responder al problema.
La exigencia de matematización se presenta en su
forma más simple cuando el individuo necesita interpretar e inferir
directamente de un modelo dado; o traducir directamente de una situación
intramatemática (por ejemplo, para identificar y seleccionar variables
importantes, recoger medidas pertinentes, hacer diagramas). La exigencia de
matematización aumenta cuando se requiere utilizar o modificar un determinado
modelo para abarcar nuevas condiciones o interpretar relaciones deducidas,
elegir un modelo familiar dentro de limitaciones y claras restricciones
articuladas, o crear un modelo donde las variables requeridas, relaciones y
limitaciones sean explícitas y claras. Un nivel aún más alto de demanda de
matematización se relaciona con la necesidad de crear o interpretar un modelo
en una situación donde muchos supuestos, variables, relaciones y limitaciones
deben ser identificados y definidos, comprobar que el modelo satisface los
requerimientos de la tarea, o evaluar o comparar modelos.
Representar:
La competencia matemática involucra muy frecuentemente representaciones
matemáticas. Esto puede suponer seleccionar, elaborar, interpretar, traducir y
usar una variedad de representaciones para captar una situación, interactuar
con un problema, o para presentar el trabajo realizado. Las representaciones
referidas incluyen ecuaciones, fórmulas, gráficos, tablas, diagramas, imágenes,
textos descriptivos y materiales concretos.
Esta habilidad matemática se asocia, en su nivel
más bajo, con la necesidad de manejar directamente una representación familiar
determinada, por ejemplo pasando directamente de texto a números o leyendo un
valor llanamente, de un gráfico o tabla. Tareas de representación con mayores
exigencias cognitivas se asocian a la selección e interpretación de una
representación estándar o familiar, en relación a una situación y en un nivel
más alto de exigencia aún, cuando requiere el uso simultáneo de dos o más
representaciones diferentes en relación a una situación, incluyendo la
modificación de una representación; o cuando la demanda es elaborar una
representación sencilla de una situación. Un nivel más alto de la demanda
cognitiva se caracteriza por la necesidad de entender y usar una representación
no estándar que requiere una importante decodificación e interpretación,
elaborar una representación que capte los aspectos claves de una situación
compleja o comparar y evaluar diferentes representaciones.
Razonar
y argumentar: Esta es una habilidad necesaria en todas las
etapas y actividades asociadas con la competencia matemática. Esta destreza
implica procesos de pensamiento arraigados que exploran y vinculan elementos
del problema para hacer inferencias a partir de ellos, conectar variables y
datos, comprobar la fiabilidad de una justificación dada o proveer una
justificación a afirmaciones planteadas.
En tareas de demanda relativamente baja para
activar esta habilidad, el razonamiento requerido implica simplemente seguir
las instrucciones dadas. En un nivel de demanda ligeramente más alto, las
tareas requieren alguna reflexión para conectar las diferentes partes de la
información, con el fin de hacer inferencias (por ejemplo, vincular componentes
separados presentes en el problema, o usar razonamiento directo dentro de un
aspecto del problema). A un nivel más alto, las tareas requieren el análisis de
la información para seguir o crear un argumento de varios pasos o conectar
varias variables, o razonar desde fuentes de información vinculadas. A un nivel
aún mayor de demanda, hay una necesidad de síntesis y evaluación de la
información, usar o crear cadenas de razonamiento para justificar inferencias o
hacer generalizaciones sobre la base y la combinación de múltiples elementos de
información.
Elaborar
estrategias: La competencia matemática frecuentemente requiere
elaborar estrategias para resolver problemas matemáticamente. Esto implica un
conjunto de procesos críticos de control que guían a un individuo a
efectivamente reconocer, formular y resolver problemas. Esta habilidad se
caracteriza por la selección o elaboración de un plan para usar Matemática,
para resolver problemas originados de una tarea en un contexto, así como guiar
su ejecución. Esta habilidad matemática puede ser demandada en cualquiera de
las etapas del proceso de resolución de un problema.
En tareas con una demanda relativamente baja de
esta habilidad, a menudo es suficiente tomar acciones directas en las que la
estrategia necesaria es indicada, conocida u obvia. En un nivel ligeramente más
alto de demanda, puede haber necesidad de decidir cuál es la estrategia
adecuada que utilice la información dada para alcanzar una conclusión. La
demanda cognitiva se incrementa con la necesidad de diseñar y construir una
estrategia para transformar la información proporcionada y alcanzar una
conclusión. Incluso las tareas más exigentes requieren la construcción de una
estrategia, elaborada para encontrar una solución exhaustiva o una conclusión
generalizada, o para evaluar o comparar diferentes estrategias posibles.
Usar
lenguaje simbólico, formal y técnico y operaciones: Ser
competente en Matemática requiere Usar lenguaje simbólico, formal y técnico y
operaciones. Esto implica comprender, manipular y hacer uso de expresiones
simbólicas regidas por convenciones y reglas matemáticas. También incluye la
comprensión y utilización de construcciones formales basadas en definiciones,
reglas y sistemas formales y también el uso de algoritmos con estas entidades.
Los símbolos, reglas y sistemas utilizados pueden variar de acuerdo a qué
conocimiento del contenido matemático particular se necesita para formular,
resolver o interpretar una tarea específica.
La demanda para la activación de estos procesos
varía enormemente a través de las tareas. En tareas simples, no necesitan ser
activadas reglas o expresiones simbólicas más allá de los cálculos aritméticos
fundamentales, operaciones con números pequeños o fácilmente manipulables. Los
trabajos con mayor demanda pueden incluir el uso directo de una relación
funcional simple, ya sea implícita o explícita (por ejemplo, relaciones
lineales familiares, fórmulas conocidas), el uso de símbolos matemáticos
formales (por sustitución directa de variables o cálculos aritméticos con
fracciones y decimales), o la activación y uso directo de definiciones
matemáticas, convenciones o conceptos simbólicos. El incremento de la demanda
cognitiva se caracteriza por la necesidad del uso explícito y manipulación de
símbolos (por ejemplo, manipulación algebraica de una fórmula), o la activación
y uso de reglas matemáticas, definiciones, convenciones, procedimientos o
fórmulas utilizando una combinación de múltiples relaciones o conceptos
simbólicos. Un nivel mayor de demanda se caracteriza por la necesidad de la
aplicación de múltiples pasos de procedimientos matemáticos formales, trabajar
en forma flexible con relaciones algebraicas o usar técnicas y conocimientos
matemáticos para producir resultados.
Usar
herramientas matemáticas: Esta habilidad que sustenta la
competencia matemática en la práctica es Usar herramientas matemáticas.
Regularmente la evaluación de la competencia
matemática ha estado basada en pruebas en papel, por lo tanto sólo ha
sido posible incluir en forma muy superficial el uso de herramientas. El componente
opcional (en el que solo algunos países participan) de la evaluación de la
competencia matemática basada en computadora para proporcionar a los
estudiantes más oportunidades de usar herramientas matemáticas e incluir
observaciones acerca de la forma en que las herramientas se utilizan como parte
de la evaluación. Las herramientas matemáticas pueden ser físicas, como instrumentos
de medición, así como calculadoras, e informáticas que se están volviendo cada
vez más accesibles. Esta habilidad implica conocer y ser capaz de hacer uso de
varios apoyos y herramientas que puedan ayudar a la actividad matemática en
proceso y, lo que es muy importante, conocer sus limitaciones. Las herramientas
matemáticas pueden, también, desempeñar un papel importante en la comunicación
de resultados.
Tareas y actividades que implican un nivel
relativamente bajo de demanda para esta habilidad pueden requerir el uso
directo de herramientas familiares, como un instrumento de medición, en
situaciones en las que el uso de esas herramientas es familiar. Mayores niveles
de demanda surgen cuando el uso de herramientas implica una secuencia de pasos
o vinculación de diferentes informaciones usando la herramienta, cuando la
familiaridad con ellas es menor o cuando la situación en la que se aplica no es
habitual. La demanda aumenta aún más cuando la herramienta debe utilizarse para
procesar y relacionar múltiples datos, cuando su aplicación se da en una
situación muy diferente de las aplicaciones familiares, cuando la herramienta
en sí es compleja y cuando se requiere una reflexión para entender y evaluar
las ventajas y las limitaciones de ellas.
Contextos
Un aspecto importante de la concepción de
competencia matemática es que se tiene en cuenta que esta área tiene
aplicaciones para resolver un conjunto de problemas que se presentan en
variados contextos. El contexto es el aspecto del mundo del individuo en el
cual los problemas se ubican. La elección de estrategias y representaciones
matemáticas apropiadas depende a menudo del contexto en el cual surge el
problema. Para el estudio son utilizados una amplia gama de contextos
auténticos lo que ofrece la posibilidad de que los estudiantes se enfrenten a
las más variadas situaciones y se conecten con una amplia gama de intereses
individuales propios del siglo XXI.
A los efectos del marco de evaluación de la
competencia matemática de PISA 2012, han sido definidas cuatro categorías de
contexto:
·
Personal:
Problemas planteados sobre actividades relacionadas con uno mismo, la propia
familia, o el propio grupo de pares y la percepción del individuo de la
importancia directa de las situaciones problemáticas en ellos. Los tipos de
contextos que pueden ser considerados personales incluyen aquellos relativos a
la preparación de alimentos, compras, juegos, salud individual, transporte
personal, deportes, viajes y finanzas personales.
·
Ocupacional:
Los problemas ubicados en un contexto ocupacional se centran en el mundo del
trabajo, pueden incluir situaciones como medición, cálculo de costos y pedido
de materiales para la construcción, nómina de sueldos y su contabilidad,
control de calidad, inventarios, diseño y toma de decisiones relacionadas con
el trabajo. Los contextos ocupacionales pueden relacionarse con cualquier nivel
de mano de obra, desde el trabajo no calificado hasta los más altos niveles de
trabajo profesional, sin olvidar que los contextos en este estudio no deben ser
totalmente ajenos a los jóvenes.
·
Social:
Los problemas planteados en un contexto social se centran en la propia
comunidad. Pueden incluir temas tales como sistemas de votación, transporte
público, gobierno, políticas públicas, demografía, publicidad, estadísticas
nacionales y económicas. Si bien los individuos están involucrados en todas
estas cuestiones de una manera personal, en la categoría de contexto social, el
foco del problema está en la perspectiva de la comunidad.
·
Científico:
Los problemas situados en un contexto científico se relacionan con la
aplicación de la Matemática en la naturaleza y en temas relacionados con la
ciencia y la tecnología. Determinados contextos pueden incluir áreas como
tiempo y clima, ecología, medicina, ciencia espacial y genética.
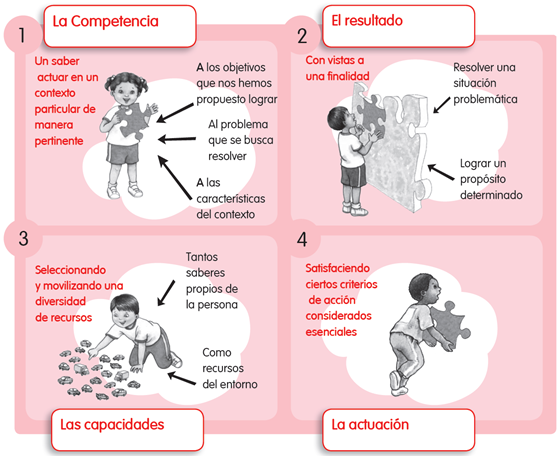
Terminología para desarrollar las competencias:
Saber actuar: Alude a la
intervención de una persona sobre una situación problemática determinada para
resolverla, pudiendo tratarse de una acción que implique sólo actividad
matemática.
Tener un contexto particular: Alude
a una situación problemática real o simulada, pero plausible, que establezca
ciertas condiciones y parámetros a la acción humana y que deben tomarse en
cuenta necesariamente.
Actuar pertinentemente: Alude a la
indispensable correspondencia de la acción con la naturaleza del contexto en el
que se interviene para resolver la situación problemática. Una acción
estereotipada que se reitera en toda situación problemática no es una acción
pertinente.
Seleccionar y movilizar saberes:
Alude a una acción que echa mano de los conocimientos matemáticos, habilidades
y de cualquier otra capacidad matemática que le sea más necesaria para realizar
la acción y resolver la situación problemática que enfrenta.
Utilizar recursos del entorno: Alude
a una acción que puede hacer uso pertinente y hábil de toda clase de medios o
herramientas externas, en la medida que el contexto y la finalidad de resolver
la situación problemática lo justifiquen.
Utilizar procedimientos basados en criterios:
Alude a formas de proceder que necesitan exhibir determinadas características,
no todas las deseables o posibles sino aquellas consideradas más esenciales o
suficientes para que logren validez y efectividad.


No hay comentarios:
Publicar un comentario
TUS SUGERENCIAS Y COMENTARIOS SON MUY IMPORTANTES POR FAVOR ESCRIBE AQUÍ